VIZUĀLO MĀKSLU ŽURNĀLS
|
|
|
| Lielais princips Inga Bunkše | |
| Lielais princips Šovasar Venēcijā līdztekus Venēcijas biennāles skatei norisinājās kāda izstāde, kas vēstīja par cilvēku mūžseno vēlmi izprast Visuma kārtību un izskaidrot visu parādību savstarpējo saistību. Tie bija Lielā principa meklējumi, kas izstādē Proportio (09.05.– 22.11.2015.) atklājās bagātīgā skaitā dažādu laiku un kultūru mākslas darbos un artefaktos. Aizraujošais kolekcionāra un mākslas dīlera Aksela Fervorta (Axel Vervoordt) un kuratores Danielas Ferreti (Daniela Ferretti) sniegums bija veltīts proporciju un zelta griezuma izpausmei visos mākslas veidos. Ekspozīcijas iekārtojums Palazzo Fortuny piecos stāvos, pils senlaicīgums, telpu konfigurācija, apskrubušās sienas piešķīra izstādei nepieciešamo mūžības auru. Mākslas darbi bija izkārtoti tā, it kā tos savā pilī būtu izvietojis tur dzīvojošs kolekcionārs, kas vismaz daļu mākslas darbu krājuma mantojis no senčiem: telpās vienkopus bija iedzīvojušies Džerolamo Fridžimelikas (Gerolamo Frigimelica) Villa Pisani projekts no 1720. gada un Lekorbizjē Villa Savoye koka modelis (20. gs. 20. gadi), Ķīnas šķīvis no 4. gs. p. Kr. un Bena Nikolsona glezna (1940), Bila Vaiolas video „Cilvēks un viņa dvēsele” (2013) un Sandro Botičelli „Sievietes portrets” (1485). Mākslas darbi, izvietoti uz antīkiem galdiem vai dārgu, bet citviet noplukušu drapēriju fona, pastiprināja iespaidu, ka tikai laimīgas nejaušības dēļ senlaicīgajā pilī sapulcināti nenovērtējami šedevri, vienlaikus rosinot saskaņu telpā un apmeklētājos. Šķiet, kuratori izstādes iekārtojumā bija izmantojuši seno grieķu kalokagatijas principu, ka viss skaistais ir arī labs. Labs tajā nozīmē, ka, rezonējot ar Visuma frekvencēm, skatītājus ieveda harmonijas pasaulē, nemanāmi virzot viņu izpratni par nemitīgo radīšanas aktu, kas arvien no jauna rada kārtību no haosa. Kas gan īsti ir zelta proporcija? Izstāde rosināja veikt īsu ekskursu zināšanās, ko cilvēce krājusi tūkstošiem gadu. Tās vienmēr ir bijušas gan progresīvas, gan cieši saistītas ar noslēpumainu mācību un reliģiskajām tradīcijām, tāpēc nereti turētas aiz atslēgas. Ticis pat uzskatīts, ka šo zināšanu nepareizai lietošanai varētu būt neprognozējamas sekas, tāpēc tās mērķtiecīgi slēptas vai pat iznīcinātas. Sakrālajā ģeometrijā valda uzskats, ka tie, kas pārzina zelta griezumu, māk to ieraudzīt un izmantot, var tuvināties Dievam, garīgumam. Visuma noslēpumi Nav zināms, kur cilvēce ieguvusi zināšanas par Lielo principu, visu lietu kārtību, bet ir saglabājies viens no seno civilizāciju brīnumiem, kurā tas iekodēts, – Heopsa piramīda Gīzā. Jau sengrieķu vēsturnieks Hērodots aprakstīja piramīdas proporciju principu – katras tās skaldnes laukums vienāds ar augstuma kvadrātu. Savukārt, izdalot skaldnes garumu ar augstumu, iegūst skaitli 1, 618 (šeit un turpmāk skaitlis noapaļots līdz trīs cipariem aiz komata). Šis skaitlis, ko sauc par zelta proporciju, minēts Rinda papirusā (1650. g. p. Kr.). Vēlāk to par godu tēlniekam Feidijam apzīmēja ar grieķu burtu φ. | |
 Kristaps Ģelzis. Pensiju akmens. Polietilēns, plastikāta līmplēve, akrila pigments. 100 × 120 cm. 2015 No izstādes „19112015” galerijā „Māksla XO” Foto: Renārs Derrings | |
| Vēl kāda no matemātiskajām sakarībām, kas skaidro piramīdas uzbūvi, saistīta ar muzikālās skaņkārtas toni la, kura skaņas viļņu frekvence ir 441 Hz. Tā ir dabā nozīmīga harmoniska rezonanses frekvence, kas ir visa saskaņas pamats. Piramīda, kas būvēta pēc matemātiskām proporcijām, darbojas kā milzīgs enerģētisks rezonators, saskaņojot cilvēka un Visuma enerģētisko procesu ritmus. Ritmam pakļauti lec un riet saule, notiek paisums un bēgums, sirdsdarbība, pulss un procesi cilvēka ķermenī ir ritmiski. Harmoniskas formas iekļaujas ritmā, neharmoniskas izsaka nekārtības. Noskaņojoties vienā ritmā ar harmonisko frekvenci, apziņa ieplūst Visuma procesos. Iespējams, piramīdas cēlāji vēlējušies nākamajām paaudzēm saglabāt šīs svarīgās zināšanas. Harmonija un samērs Senās zināšanas par Visumā valdošajiem samērības principiem rakstiski formulēja Pitagors (6. gs. p. Kr.). Viņš kā visu lietu pirmsākumu meklēja skaitli, ar kura palīdzību skaidrot likumus, kas izteiktu pasaules esību un kārtību. Pitagora skola ar skaitliskajām attiecībām noteica un skaidroja gan kosmosa uzbūvi, gan dabaszinātnes, gan estētiku un mūziku, atzīstot, ka visas lietas ir veidojušās, ievērojot harmonijas principus. Zināšanas Pitagors klasificēja, radot simbolu Tetraktys – vienādmalu trīsstūri. Katru trīsstūra malu veido četri punkti vienādos attālumos, centrā ir viens punkts. Viens, pēc Pitagora uzskatiem, nav skaitlis, bet vienība, no kuras izriet visi skaitļi, kas ietver visa iespējamā potencialitāti. Saskaitot visus plaknes punktus, iegūst skaitli desmit. Ar pirmajiem desmit skaitļiem var izteikt visus pārējos skaitļus un skaitliskās darbības. Atbilstoši ar tetrakti pēc Pitagora izveidotās sistēmas var izteikt kosmosa uzbūvi, muzikālās harmonijas, skaitļu pāra un nepāra progresijas, sabiedrības uzbūvi un vēl citas – kopā vienpadsmit – sakarības noteiktā hierarhiskā sistēmā. Tetraktī visi elementi ir cieši saistīti, savstarpēji līdzsvaroti un veido sabalansētu struktūru, ietverot visu universālo gudrību. Domu par harmoniju un samēru tālāk attīstīja Platons. Darbā „Tīmajs” viņš rakstīja: „Dievs, gribēdams padarīt pasauli cik vien iespējams līdzīgāku skaistākajai no iedomājamām esībām un iespējami pilnīgāku it visā, radīja to kā vienu redzamu veidojumu, tā ka visi pēc dabas tam radniecīgie veidojumi satilpst tai vienā.” Samērības principu Platons skaidroja šādi: lai savienotu divas daļas vispilnīgākajā, visracionālākajā veidā un no tām izveidotos trešā, nepieciešama proporcija, kas tās sastiprinātu vienā veselā. Turklāt vienas daļas attiecībai pret otru jābūt tādai pašai kā veseluma attiecībai pret lielāko daļu, piemēram, 1:2 = 2:3. Platona skolnieks Eiklīds darbā „Elementi” pirms 2300 gadiem aprakstīja daļas un veselā attiecības: divi objekti ir zelta attiecībās, ja to attiecība ir tāda pati kā attiecība starp to summu un lielāko no abiem objektiem. | |
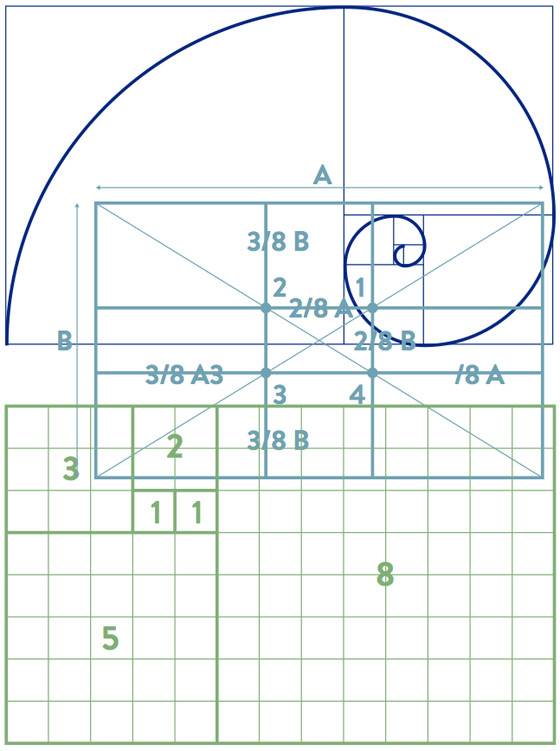 Fibonači spirāle. Laukuma dalījums atbilstoši zelta griezumam 61,6 % pret 38,3 % Zelta griezumam atbilstoša taisnstūru kopa pēc Fibonači skaitļu rindas Zīmējums: Anitra Eglīte-Poikāne | |
| Senie grieķi meklēja ideālo skaistumu un, veidojot skulptūras, sintezēja zināšanas par skaistu un samērīgu ķermeni. Tēlnieks un teorētiķis Polikleits 5. gs. p. Kr. izstrādāja kanonu, nosakot ķermeņa ideālo proporciju likumus. Pagāja simt gadu, un tēlnieka Prāksitela skulptūrās apvienojās ķermeņa un dvēseles skaistums, sasniedzot kalokagatiju – seno grieķu ideālu (gr. kalokagathia; kalos – skaists, agathos – labs). Grieķi perfekcijai tuvināja atveidotos dievu ķermeņus, bet viduslaiku kristīgā pasaule uzskatīja, ka viss Universs ir skaists, jo to radījis Dievs. Zālamana gudrības grāmatā teikts, ka Dievs radījis pasauli pēc mēra, skaita un svara, tātad vispirms Dievs radījis universālos likumus, pēc kuriem tad no matērijas veidojis pasauli. Akvīnas Toms rakstīja, ka „skaistums rodas ne tikai no tā, ka ikviena lieta paliek nemainīga, bet arī no tā, ka tās visas savienojas vienotā kopumā, katra atbilstoši savām īpašībām”. Tātad tikai mijiedarbībā atklājas lietu skaistums, kas viduslaikos visuzskatāmāk izpaudās gotiskajās katedrālēs. Universālie likumi atspoguļojās gan dabas, gan cilvēku radītajā. Fibonači sekvence Zelta griezuma mūsdienu matemātiskā pamatojuma pamatlicējs ir izcilais itāļu matemātiķis Fibonači (ap 1170–ap 1250). Līdz atklājumam viņš nonāca, risinot matemātikas uzdevumu par trušu vairošanos. Uzdevumā bija jāaprēķina, cik trušu būs pēc gada, ja ir viens trušu pāris, kam ik mēnesi piedzimst vēl viens trušu pāris. Fibonači izmantoja vienkāršus aprēķinus. Sākumā ir viens trušu pāris, otrā mēneša beigās trušu pārim piedzimst divi truši, tātad kopā jau būs divi pāri. Trešā mēneša beigās pirmajam pārim piedzims otrs pāris, kopā būs trīs pāri trušu. Ceturtā mēneša beigās pirmajam pārim atkal piedzims trušu pāris, bet trušu pāris, kuri dzimuši otrā mēneša beigās, radīs savu pirmo pēcnācēju pāri, tātad jau būs pieci pāri trušu. Turpinot aprēķinus, Fibonači atklāja skaitļu rindu, kurā katrs nākamais skaitlis ir divu iepriekšējo summa: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987. Attiecības ar zelta skaitli φ ir šādas: divu secīgu Fibonači skaitļu dalījums pretējā virzienā (lielākajam pret mazāko) ir tuvs zelta griezumam 1,618. Izvēloties lielākus Fibonači skaitļus, rezultāts maksimāli tuvosies skaitlim φ, piemēram, 233:144 = 1,61805555. Visvienkāršāk sakarību izprast, uz rūtiņu papīra uzzīmējot zelta griezumam atbilstošu taisnstūru kopu, kas atbilst Fibonači rindai. Savienojot izveidoto kvadrātu pretējos stūrus ar liektu diagonāli, iegūstam Fibonači spirāli. Gēte uzskatīja spirāli par ģeometrisku simbolu dzīvei un garīgai attīstībai, vienai no visu organismu raksturīgākajām pazīmēm, esamības būtībai. Pa spirāli aug augu dzinumi, izvietojas sēklas saulespuķē, adatas kaktusā. DNS molekulas, cilvēka ģenētiskās informācijas nesējas, arī veido spirāli, spirāle atrodama galaktiku sistēmu un mikroorganismu uzbūvē. Zelta griezums ir iracionāls skaitlis, kas atspoguļo proporciju iracionalitāti dabā, un tas iegūst savu nozīmi tikai salīdzinājumā ar Vienu. Fibonači skaitļu rinda atspoguļo veselumu un racionalitāti. Abu savienojums simbolizē divu pretstatu vienību – nepārtrauktību un daļu, kustību un miera stāvokli, vīrišķo un sievišķo, garīgo un materiālo. Ar skaitļu palīdzību iespējams izprast pasaules uzbūvi. Tie izsaka pamatlikumu un piedāvā risinājumu esības pamatjautājumiem. Dievišķā proporcija Renesansē zelta griezums tika pacelts galvenā estētiskā principa augstumos. Lielie meistari vienlaikus bija mākslinieki un zinātnieki. Leonardo da Vinči, Rafaēls un Mikelandželo apzināti izmantoja zelta griezumu, jo zināja tā iedarbību uz skatītāju. „Bez matemātikas nav mākslas,” uzsvēra Luka Pačoli, franciskāņu mūks un renesanses matemātiķis, kurš, iedvesmojies no Platona darba „Tīmajs”, Fibonači, citu antīko un viduslaiku domātāju sacerējumiem, no jauna gaismā izcēla universālās ģeometriskās likumības un nosauca tās par Dievišķo proporciju (De divina proportione, 1509). Izdevumu papildināja 60 pēc Leonardo da Vinči gravīrām izgatavotas ilustrācijas, kas attēloja Platona trīsdimensionālās regulārās figūras jeb Platona ķermeņus. Platons uzskatīja, ka māksla ir tikai patiesā skaistuma nepilnīgs atdarinājums un tāpēc nepieciešams pievērsties ģeometriskajām formām. Pieci darbā „Tīmajs” analizētie ķermeņi, kas iemieso Universa matemātisko koncepciju, ir kubs jeb heksaedrs, ikosaedrs, tetraedrs, oktaedrs un dodekaedrs.. Arheoloģiskie un zinātniskie atklājumi liecina, ka šādus arhetipiskos pasaules uzbūves modeļus pazinuši gan senie ēģiptieši, gan eiropieši. Sakrālajā ģeometrijā valda uzskats, ka ģeometriskie simboli ir vizuāli instrumenti, kas palīdz saskaņot cilvēka ķermeniskās un garīgās svārstības ar dabas harmoniskajiem ritmiem. Proporcija ģeometriskās figūrās, mūzikā un matemātikā tika saprasta kā harmoniska attiecība starp daļām un daļas attiecība pret veselo. Šī attiecība tika izteikta ar jau zināmo skaitli: AB/CB = CB/AC= 1,618 Pačoli savā grāmatā iztirzā Vitrūvija (1. gs. p. Kr.) darbu „Traktāts par arhitektūru” (Trattato dell’architettura), kurā romiešu arhitekts apcerēja cilvēka ķermeņa ideālās proporcijas un to saistību ar arhitektūru. Vitrūvija uzskati ievērojami ietekmēja citu renesanses mākslinieku un arhitektu uzskatus, par to liecina ne vien populārais Vitrūvija cilvēka zīmējums, kurā autors Leonardo da Vinči attēlojis cilvēka ķermeņa analoģiju ar Visuma darbības principiem. Arī arhitektu Leona Batistas Alberti De re aedificatoria (1452) un Andreas Palladio I quattro libri dell’architettura (1570) paustie uzskati par samēru ierosmi guvuši Vitrūvija idejās. | |
 Guntars Sietiņš. Levitācija Nr. 18. Fotogravīra Plate 12 × 12 cm, lapa 35 × 50 cm. 2011 | |
| Vācu astronoms Johanness Keplers (1571–1630) arī aizrāvās ar harmonijas likumību pētīšanu, zelta dalījuma principu salīdzinot ar ģeometrijas dārgakmeni, un pirmais izpētīja filotaksi – auga detaļu harmonisku izvietojumu atbilstoši Fibonači skaitļu rindai. Tomēr kāds cits dižā astronoma atklājums, lai arī balstīts uz matemātiskiem aprēķiniem un pirmo reizi definētām cēloņsakarībām, satricināja līdzsvaroto pasaules uzskatu, radot priekšnoteikumus jaunas sapratnes izveidei par laiku un telpu: viņa planetārajā modelī Zeme ap Sauli riņķo pa elipsi, nevis koncentrisku apli, kā domāja iepriekš. Parādījās spriedumi, kas, balstīti uz dabas novērojumiem, noliedza proporcionalitāti kā skaistuma un harmonijas izteicēju (Edmunda Bērka „Filozofisks pētījums par cildenā un skaistā ideju izcelsmi”, 1756). Pasaule uz laiku zaudēja interesi par ģeometrisko sakārtotību. Tikai 19. gadsimta vidū līdz ar Ādolfa Ceizinga (Adolf Zeising, 1810–1876) darbu „Jaunā teorija par cilvēka ķermeņa proporcijām” (1854) atsākās mākslas vēstures aizraušanās ar zelta griezumu. Apjomīgajā pētījumā, kas bija balstīts uz dabas novērojumiem un iepriekšējo gadsimtu filozofu un pētnieku darbiem, vācu psihologs un matemātiķis parādīja zelta griezuma kā universālā likuma klātesamību bioloģijā, botānikā, matemātikā, vēsturē, arhitektūrā, mākslā, vispilnīgāko realizāciju rodot cilvēka ķermenī. Ceizinga un citu vēsturisko pētījumu rezultātus apkopoja franču arhitekts Lekorbizjē (1887–1965). Viņa izstrādātā Modular sistēma balstījās uz cilvēka auguma un telpas sakarībām zelta griezuma attiecībās. Harmonija ir universāls princips, kas nodrošina cilvēka organisma funkcionalitāti un adaptāciju pasaulē. Funkcionālo sistēmu savstarpēji atkarīgās attiecības saskan ar zinātni par fraktāļu struktūru, kas ir pamatā pasaules uzbūvei un atbilst zelta griezuma likumsakarībām. Šīs likumsakarības attēlo cilvēka iekšējo harmoniju un attiecīgi izpaužas kā cilvēka adaptācija ārējai pasaulei. Mākslā un arhitektūrā sameklējami neskaitāmi piemēri zelta proporciju izmantojumam. Mūziķi izsenis izmantojuši ne vien muzikālās harmonijas, bet, lai izraisītu spriegumu, nemieru, disonansi, arī, piemēram, palielinātas kvartas intervālu do-fa diēzu, ko pat dēvēja par diabolus in musica. Zelta griezumu filmas „Bruņukuģis Potjomkins” montāžā lietojis Sergejs Eizenšteins, bet Andrejs Tarkovskis ne reizi vien izmantoja ar zelta griezuma skaitli aprēķinātu, bet izmainītu ritmu, lai filmās izjauktu objektīvajā realitātē balstītu laika ritējumu. Uztvere Cicerons teicis, ka „dvēsele līdz ar acīm pierod pie tā, ko redz pastāvīgi, un nemeklē vairs tā cēloņus”. Arī mākslinieki, reiz apguvuši kompozīcijas pamatlikumus, vairs neizmanto ģeometrijas pamatlikumus mākslas darba konstruēšanā. Daudzos gadījumos apzināts šīs proporcijas lietojums paplašina izpratni par skaisto, līdzsvaru un harmoniju un izraisa atbilstošas izjūtas skatītājā. Tomēr mūzikā ar harmoniju apguvi nepietiek, lai komponētu skaņdarbus, un, apgūstot krāsu mācību, par mākslinieku vēl nekļūst. Mācība par proporcijām ir svarīga kā tehnisks paņēmiens, lai saprastu, kā uzbūvēt darbu, bet proporciju apguve vēl nenozīmē gatavību mākslas darbu radīšanai. Māksla augstākajā pakāpē nekad nav pašizteiksmes līdzeklis, bet veids, kā izteikt garīgumu, un uzlūkojama par tiltu starp galīgo un bezgalīgo, pa kuru tas, kurš veltījis sevi mākslai, mēro ceļu uz citām realitātēm. Mākslinieks, kurš vēlējies piekļūt radīšanas brīnumam, kļūst par kādas augstākas gribas tulkotāju, „otu Dieva rokās”, kas universālās garīgās struktūras, atrastas intuīcijā, pārnes vizuāli tveramās formās. Šajās intuitīvajās atklāsmēs forma nereti kļūst sekundāra. Vēl vairāk – tā var tikt transformēta, lai izceltu būtiskās īpašības, nevis glītu ārpusi. Forma, ko cilvēks uztver ar redzi, nepastāv tieši tajā veidolā, bet ir zināšanu objekts. Forma netiek vērtēta kā pati par sevi, bet tikai tik daudz, cik tā spēj izteikt augstāko ideju. Jebkura mākslas darba materialitātes derīgums atkarīgs no tā, cik daudz tas spēj attēlot garīgo realitāti. Forma un estētiskā bauda ir cieši un loģiski saistītas. Atslēga, lai saprastu šo iekšējās loģikas saiti mākslas darbā, ir zelta griezums. Mākslinieki, kas šodien izzina acīm un citām maņām netveramo pasauli, uz datora ekrāna projicējot elektromagnētiskos viļņus, vai iegūst savdabīgus portretus, raidot lāzera staru cauri konkrēta cilvēka asins pilienam, tāpat kā Leonardo da Vinči laikos, ir reizē dabas atdarinātāji un jaunradītāji. No vienas puses, viņi tikai pārraida neredzamās dabas attēlus, balstoties uz sava laika zinātniskajiem atklājumiem, no otras, – izmanto iztēli un tehniskus jaunievedumus, lai iegūtu estētiski baudāmu attēlu. Katrā no šādi tapušiem darbiem nepastarpināti atspoguļojas kaut kas no Lielā principa. Cilvēka apziņa ir cieši saistīta ar laiktelpu, kurā tas atrodas. Mūsdienu mākslinieki nākotnei atstās sava laika nospiedumus, bet, tāpat kā no Leonardo da Vinči laikiem, atmiņā saglabāsies tikai to darbi, kuri būs pratuši ielūkoties neierobežotajā Visumā un sabalsoties ar tā enerģētiskajiem procesiem, ne vien izgatavojuši sava laika materialitātes pārnesumus. Un nebūs svarīgi, vai šedevri tapuši matemātisku aprēķinu rezultātā vai ar dievišķās intuīcijas starpniecību. Ilustrācijai izmantotas Latvijas mākslinieku darbu reprodukcijas no izstādes „Saules sistēmas perspektīva” (2014) kataloga. Paldies izstādes kuratorei Elitai Ansonei un Latvijas Nacionālajam mākslas muzejam, fondam „Zentas Loginas muzejs” un galerijai „Māksla XO”, kā arī reproducēto darbu autoriem. Izmantotie avoti: Helms, Ina. Golden ratio discovered in a quantum world. www.eurekalert.org/pub_releases/2010-01/haog-grd010510.php The Thirteen Books of Euclid’s Elements. Chicago, 1952. Zeising, Adolf. Neue Lehre von den Proportionen des menschlichen Korpers. Leipzig, 1854. Lawlor R. Sacred Geometry. Philosophy and Paradise. London, 1995. Par Johannesu Kepleru: kepler.nasa.gov/Mission/ JohannesKepler/. Kundziņš, Māris. Dabas formu estētika: Bionika un māksla. Rīga, 2004. Vipers, Boriss. Laika problēma tēlotājās mākslās. No: Mākslas likteņi un esejas. Rīga, 2005. Hokings, Stīvens. Mlodinovs, Leonards. Vēl īsāk par laika vēsturi. Rīga, 2007. Eko, Umberto. Skaistuma vēsture. Rīga, 2009. Siliņš, Edgars. Lielo patiesību meklējumi: esejas. Rīga, 2006. Эйзенштейн, Сергей. Неравнодушная природа. Том 1: Чувство кино. Москва, 2004. Неаполитанский С. М., Матвеев С. А. Сакральная геометрия. СПб., 2004. Платон. Тимей. Pieejams: www.plato.spbu.ru/TEXTS/ PLATO/timaios.htm. https://en.wikipedia.org/wiki/Penrose tiling | |
| Atgriezties | |